Introduction

I originally started this project when watching this video, and I was really intrigued by the idea of creating a chess engine that can beat anyone. I have already had my fair share of experience with different algorithms, and dipped my feet into competitive programming, so this really felt like the perfect project. Before we get into the technical stuff, I’ll show a demonstration of an engine-vs-engine game. This is a game against maia9, a AI-based engine based on games of 1900-rated players.

I’m happy to say that my engine (black) crushed maia.

Features/Table of contents

Building a chess engine has led me down a massive rabbithole, since no matter what you add there will always be some way to add more elo. I had to limit myself somewhere, and by the end these were the features I decided to add (click on feature for explanation):

Engine features

Bitboards
Move generation
SIMD Optimizations
Material evaluation
Minimax/Negamax
Alpha-Beta pruning
Move ordering
Piece-Square tables
Quiescence Search
Principal Variation Search
Nullmove pruning/heuristic

Program features

Rust macroquad frontend
UCI Integration
SPRT testing

Bitboards

The most important part of a chess engine is the board representation, since that is what all other operations will use to base their transformations. The most efficient known method to represent a board through having an array of 64 bit integers, and where each bit signifies a certain square on the board.

For example to represent white pawns on the start rank then the bitboard would show 0b0000000011111111000000000000000000000000000000000000000000000000 (binary representation). This kind of board representation is super useful because we can do tons of complicated operations with just a single binary op.

If we want to check what pawns a black queen can capture (without considering blocking pieces), we can take the queens attack-bitboard and AND it with bb_pieces[white][pawn]. (click here website used for visualizing bitboards)

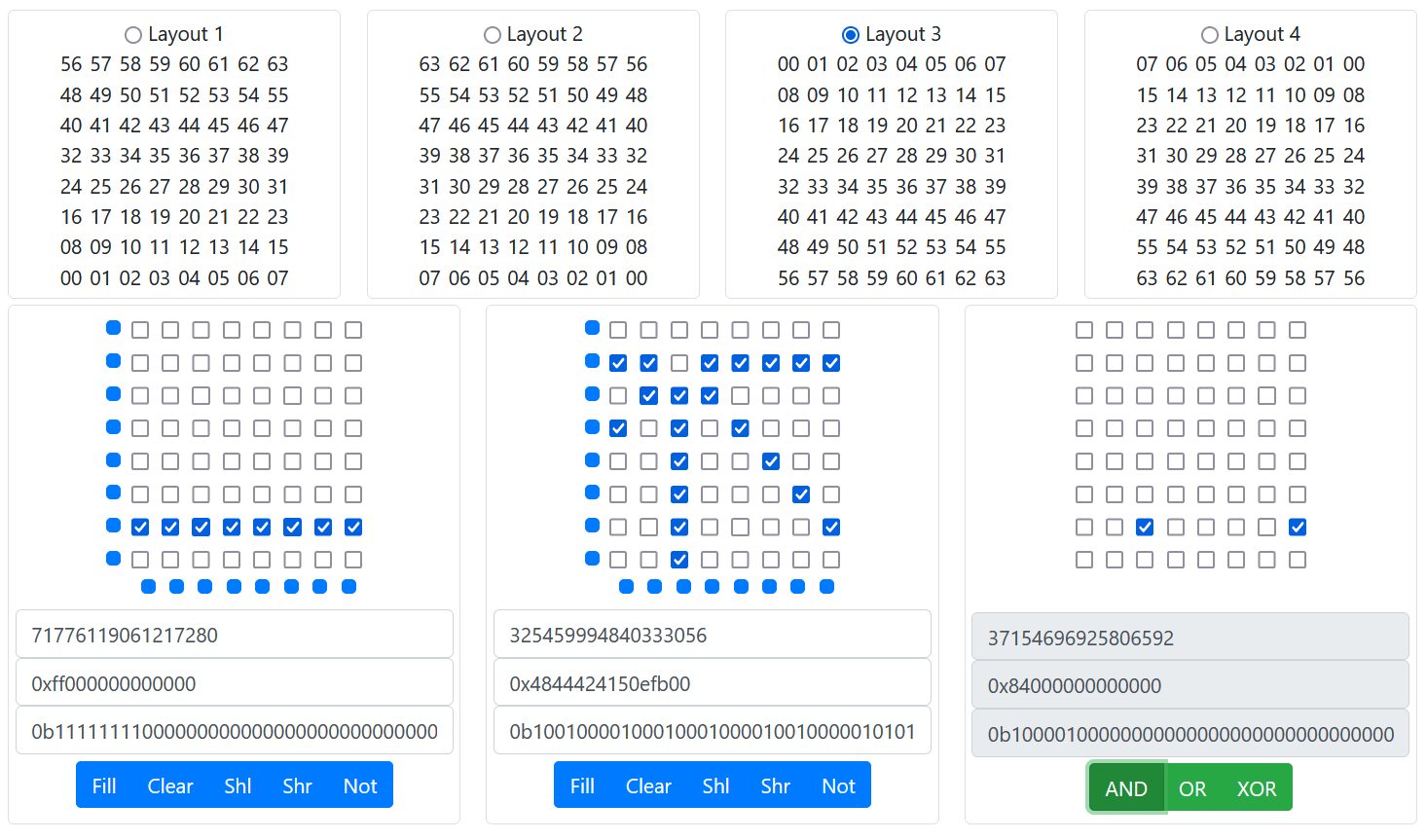
Bitboard visualization with queen attack bitboard being ANDed with pawn bitboard

This is how my board struct looks

pub struct Board {
    pub bb_pieces: [[Bitboard; 6]; 2],
    pub bb_side: [Bitboard; 3],
    pub game_state: GameState,
    pub history: History,
    pub piece_list: [Option<Piece>; 64],
    zobrist_randoms: ZobristRandoms,
}

if you ignore all the other stuff, you can see that I have a 12 bb_pieces, 6 bitboards for all white pieces and 6 bitboards for all white pieces. My bitboards start at top-left and go downwards. I also created three bitboards to check for all white pieces, all black pieces and all black pieces. These are “aggregate bitboards”. They can be computed with just AND-ing all bb_pieces, but since we access these so often it is more efficient to have them all ready to go.

Move Generation

At the core of the engine, is the move generation, the chess itself. Given a board position and side, we need to be able to get all legal moves, and then be able to do and undo those moves.

Leaping pieces (knight and king)

The knight and king is easy to generate moves from. We can just make a bitboard for each square that for instance the king can be at, so 64 bitboards. I just wrote a python script to generate these bitboards. Then we hardcode that array of 64 bitboards per leaping piece into the code, and when we need to generate rook moves for a certain square, we index into that array, and AND it with the inverse of our sides bitboard (so that we can’t capture our own pieces).

Sliding pieces

These are a lot harder to implement due to the fact that we have to stop move generation for that piece on a side when we encounter a piece. We need to stop just before a piece of ours, and on a piece of theirs. This could be fixed with a concept called “Magic Bitboards”, and would increase performance by around 20-30%, however that is pretty complicated to implement for not enough gain, so I just used a primitive for loop, that is sufficient for competitive play.

Pawn moves

The pawn moves were the hardest, due to the fact that we could have en-passant and that attack and forward and attack isn’t the same. I first used the sliding approach for the 1/2 forward moves, and then just offset the attack bit and ANDed it with opponents pieces. I could have instead used bitboard array for attack pieces, but if it works it works. The pawn attacks count all of the opponents pieces as valid targets, aswell as the en-passant square that is stored in the gamestate.

Avoiding checks

This is the hardest part of move generation, and takes up the largest time in move generation, and why gen_moves is so so much faster than gen_legal_moves. My solution is to for each move:

Do the move
Generate attack bitboard for opposite side
AND the attack bitboard with our king (checking if our king is under check)
If it is, (result is non-zero), the move is invalid
Undo move

Testing move-generator

To test my movegen, I created a routing to recursively generate moves to a certain depth, and count all the leaf nodes. This is called as perft-testing and is an essential part of verifying the correctness of a move generator. I have both the benchmarker submodule and perft unit testing on the engine, as the move generator is the most common source of bugs in chess engines. I tested my perft against stockfish, but you can also use webperft to test your perft. There is a great collection of test positions on the Chess Programming Wiki.

SIMD Optimizations

Another reason why bitboards are so effective are CPU hardware optimizations when doing things like finding the first/last one, counting ones in an integer, etc. This is also why it’s so important to always compile with targeting modern CPUs, since the engine will have a day and night difference between performance with and without SIMD.

When we look for pieces we don’t have to go through every 64 bits looking for ones, there are the POPCNT family of instructions originally introduces in the SSE4 x86 extension (and equivalents for newer ARM cpus). That allow us to in constant time count ones, find leading/traling ones or zeros.

For example an expression like the following

num.count_ones()

will compile to this without Streaming SIMD extensions

mov     rcx, rdi
mov     qword ptr [rsp - 24], rcx
mov     qword ptr [rsp - 16], rcx
mov     rax, rcx
shr     rax
movabs  rdx, 6148914691236517205
and     rax, rdx
sub     rcx, rax
movabs  rdx, 3689348814741910323
mov     rax, rcx
and     rax, rdx
shr     rcx, 2
and     rcx, rdx
add     rax, rcx
mov     rcx, rax
shr     rcx, 4
add     rax, rcx
movabs  rcx, 1085102592571150095
and     rax, rcx
movabs  rcx, 72340172838076673
imul    rax, rcx
shr     rax, 56

and will compile to a loop like the following with the extensions:

popcnt  rax, rdi

quite the difference.. I think this is a nice example of the power of hardware optimizations vs software optimizations, the first example is branchless and is doing it’s best to optimize the expression, but no matter how hard it tries it will never beat the popcnt.

Material evaluation

Now that we have a working move generator, we can start making the engine play moves. The most primitive way to make the best move is to just do each move, evaluate a position then undo it. So the move that leads to the best Material Evaluation will be the best move.

Material evaluation is just adding upp all pieces on the board, and adding points for each piece (eg. Queen = 900 points, Pawn = 100 points). A depth-1 material evaluation is not really a powerful engine tho, as a human with the iq of a desert rat could easily win against this computer.

We represent the evaluation as positive numbers will be good for white, and negative will be good for black.

Minimax/Negamax

Minimax

What if we want to search further than a depth of 1, we clearly need a better method, and that’s where Minimax comes in. We have two sides that are trying to achieve different goals, white the maximising side and black, the minimising side.

The idea is that we will do the move that will lead to the best evaluation if the other side does the best move (worst move for us) aswell.

Take this pseudocode as an example:

def maxi(depth):
    if depth == 0:
        return eval()

    maxScore = -INF
    for move in moves:
        do(move)
        score = mini(depth - 1)
        maxScore = max(score, maxScore)
        undo(move)
    return maxScore

def mini(depth):
    if depth == 0:
        return eval()

    minScore = INF
    for move in moves:
        do(move)
        score = maxi(depth - 1)
        minScore = min(score, minScore)
        undo(move)
    return minScore

There are two routines, one is responsible for maximising the score, and the other one for minimising. So the depth-n evaluation is the maxi(n) if side to move is white, and mini(n) if the side to move is black.

Negamax

It is pretty annoying to have to maintain two functions, especially as the scope of the search will grow and we add features that will prune and reduce the search tree. That’s why it’s a lot more common to use negamax (one function), instead of minimax (two functions). This will return the exact same evaluation, but with much easier code.

The idea of negamax is that it will always try to maximise no matter what, and instead of having a separate mini function, it just negates the maximisation of the other side.

In my implementation I don’t flip the eval based on color in the negamax/quiescence, but rather at the static eval node.

def negamax(depth, color):
    if depth == 0:
        return color * eval()

    maxScore = -INF
    for move in moves:
        do(move)
        score = -negamax(depth - 1, -color)
        maxScore = max(score, maxScore)
        undo(move)
    return maxScore

This is a lot easier to maintain and add features to, and the real modified negamax including all features will definitely be a lot bigger.

Alpha-beta pruning

Observe that in negamax, we play assuming that the opposite side will play the best move, and we evaluate based on that. However this means that we will be able to skip on a lot of unnecesary researches. Take the following image as an example, where the dark-gray nodes are pruned.

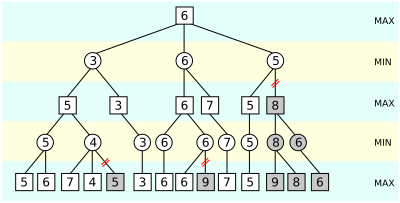
Notice that when we get the evaluation of 4, we know that it’s such a low evaluation, that the maximising side would never allow for this position to happen (since we always assume both sides play optimally), since they can force the left branch instead, and could pick 5 instead. This doesn’t seem like a massive difference in the performance, but the deeper we go, and the larger the initial branching factor is (and the better our move overing is), the more efficient this gets.

Alpha-beta pruning could eliminate the vast majority of our leaf nodes, and still leave us with the same final evaluation line. Not only this, but it also unlocks a whole lot of new possibilitys such as looking for an evaluation within a range (and checking if it falls within that range), and checking if a move is better or worse than a certain eval.

It is actually implemented pretty easily, just by having a lower and higher bound as a parameter to the negamax function (alpha and beta), and then returning early when the eval falls outside that bound.

To implement alpha-beta search add alpha and beta as parameters to your negamax function, and then add these conditions to your negamax.

if score > best_score {
  best_score = score;
  best_move = mv.clone();
  if ply == 0 {
    self.best_move = Some(*mv);
  }

  if score > alpha {
    alpha = score; // Set lower bound
    if alpha >= beta {
        break; // Prune
    }
  }
}

Fail-soft vs Fail-hard

There are two ways to fail, fail-soft and fail-hard. Fail-soft is often preferred since it prunes more aggressively, although it does introduce increased search instability. This is often a dichotomy you will be faced with in chess programming, search instability is impossible to avoid if you want performance. It is usually better to go with performance instead of more stability, although you should SPRT test all decisions like this (which i go over later in the article).

Move-ordering

Most Valuable Victim - Least Valuable Aggressor (MVV-LVA)

This is the most simple way to order moves, which is by first sorting it by the most valuable victim, then the least valuable agressor. This will help you easily catch good trades and hanging pieces, and it will prune a lot of nodes. This is a faster and less accurate way to sort moves.

Static Exchange Evaluation (SEE)

This is a more accurate move-ordering technique but a lot more resource intensive, and if it will prune more than it will cost is up to testing. This will order moves by the moves that will do the best exchange first. Imagine the engine doing takes-takes-takes analysis on a single square and then adding upp the wins and losses.

I tested MVV-LVA and SEE, and it ended up that MVV-LVA outperformed SEE, however I have since then optimized my movegen and search a bit, and it is possible that the weights have flipped in favor of SEE.

Piece Square Tables

These search features will make the engine good at finding the best path to a decent evaluation, but they are not that great if you consider that at this point we still evaluate by materials. A chess engine is built up of Search and Evaluation, so to make it perform better we need to reward it for certain behaviours and punish it for others.

A great way to do this are piece-square tables, that reward certain pieces for going to certain squares, and punish them for others. This punishment should be enough to attract pieces to good positions, but not for “no reason”, aka if it sees a better tactical moment like forcing a win of pieces it shouldn’t give it up for just “more center control” or whatever.

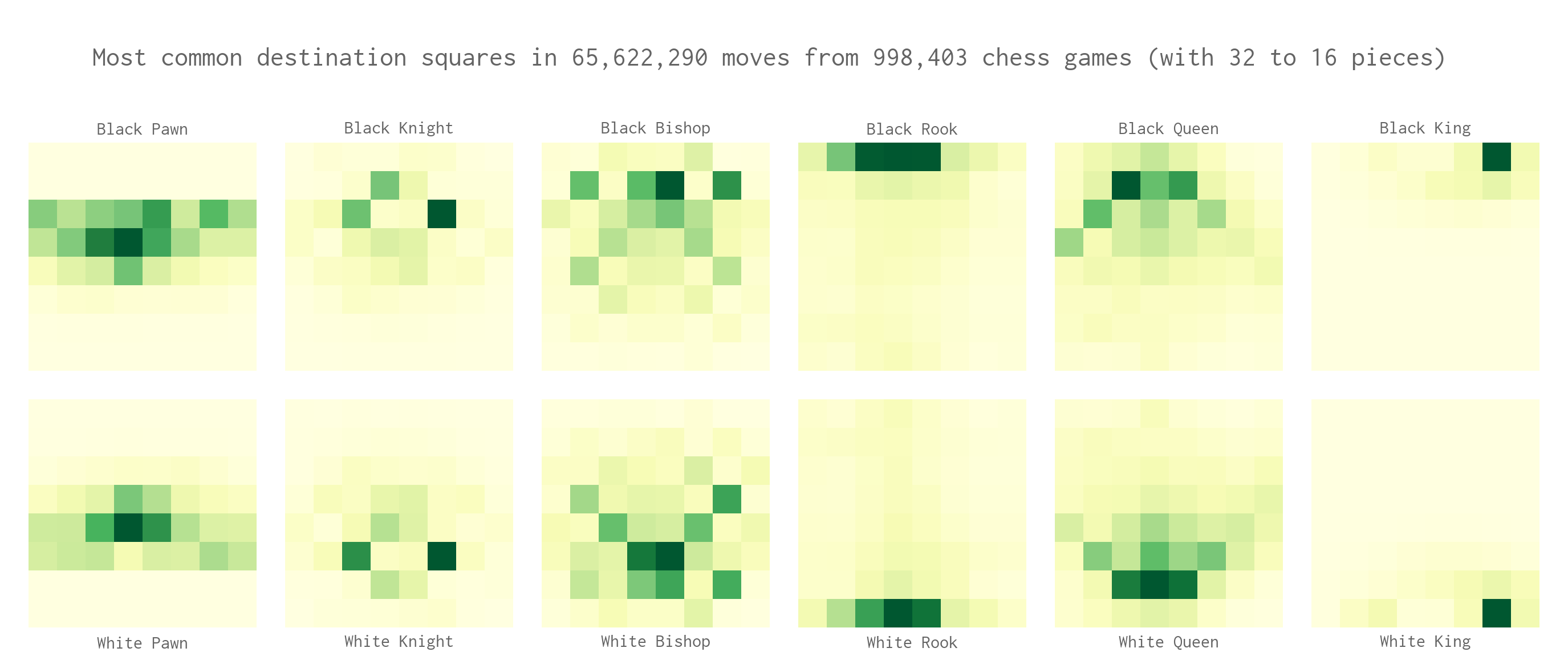
This map of destination pieces, could be used as a table that will attract pieces into positions where they take more center control. and the black versions of the tables, are flipped. The weights for my tables aren’t taken from a statistical analysis like this, but instead I use the classic PESTO weights that are optimized for use when you rely heavily on your PSQT-s for evaluation.

Tapering your eval

You will want your pieces to be attracted differently in the middlegame and the endgame, like for example the king should want to be in the middle during an endgame (as it is harder to checkmate, and it gives more control), but at the corners during openings and midgame (as it is more safe there).

pub fn get_phase(&self, board: &Board) -> i32 {
    let phase_values = [0, 1, 1, 2, 4, 0];
    let mut phase: i32 = 24;

    for side in 0..2 {
        for piece in 0..6 {
            phase -= phase_values[piece] * (board.bb_pieces[side][piece].count_ones() as i32);
        }
    }

    ((phase * 256) / 24).max(0)
}

My phase calculation is pretty simple, as it just starts at 256 and removes points for each piece on the board (making it that a phase number is higher, the further you are into the endgame).

Then I use that to taper the piece square tables, between their endgame preferred and midgame preferred positions. To increase performance, I cached the following function for each possible game phase from 0 to 256.

pub fn apply_weight(&self, midgame: [i32; 64], endgame: [i32; 64], weight: i32) -> [i32; 64] {
    let mut out = [0; 64];

    for square in 0..64 {
        out[square] = (midgame[square] * (256 - weight) + endgame[square] * weight) / 256
    }

    out
}

Quiescence Search

To prevent the so-called “horizon effect” where a move looks like a good move in depth-1, but can easily be undone (such as capturing a pawn with a queen, when it can just be captured back next move), you can add a quiescence search function that only considers captures (some engines let it promote aswell), and that will give you massive gains compared to the tradeoff of expanding the search tree. When you hear that engines spend most of their time “quiescing”, this is what that means.

The quiescent search is also a negamax alpha-beta search, but it only contains capture moves. It also has a stand-pat to exit early if it’s static eval is better than beta (fails high).

TLDR is:

Run negamax with only capture moves
For each run of the function, prune at standing pat, aswell as depth 0

Principal Variation search / Null Window Search

Remember how the Alpha-Beta lets us search for evaluations that are inside a range? Now imagine, we take a very small window (alpha, alpha+1), and search inside that window. Then when you get your evaluation back, you check if it failed high (pruned at/above alpha+1) or low (at/below alpha). This would tell you if this positions evaluation is above or below a certain value.

Observe how a large majority of positions will fail low/be too bad, and if we can do a much faster “null window search”, beforehand we can quickly discard the moves that are clearly too bad.

for move in moves:
  score = negamax(depth, alpha, alpha+1)
  if score > alpha:
    score = negamax(depth alpha, beta)
  else:
    continue
  ...

Null move pruning

If we want to take a quick shortcut to check if a whole position will fail low, we can take another obsevration in mind: In almost all positions (except for a zugzwang), doing no move at all is worse than doing your best move. This means that if we run a null move (we can run it at reduced depth too without too much search instability), as a null window search we can prune many fail-low positions as a fail low.

Checking for zugzwangs

Most zugzwang positions will be pawn-only, which means that we can just do a check for if we only have pawns and kings left, this can be done with a shifty bitboard method like before, where we AND our kings and pawns together, and compare it to bb_side[US]. We should also put limits on how deep we need to be in the search tree before we start nullmove pruning, so that we don’t discard vital positions that are close to our root evaluation. We also check for checks, and against doing two null-moves in a row.

My full guard condition for nullmoving:

if !in_check
    && estimation >= beta
    && depth >= 3
    && ply > 0
    && board.game_state.can_nullmove
    && alpha == beta - 1
    && board.bb_side[board.us()]
        != board.bb_pieces[board.us()][Pieces::KING]
            | board.bb_pieces[board.us()][Pieces::PAWN]

Late move reductions

When we are late into our search tree, we can reduce the search window for non-critical positions to squeeze out more performance. How much we can reduce by is dependent on engine to engine, and is calculated through this formula.

let mut reduction = if can_reduce {
    pub const CONSTANT: f64 = 2.78;
    pub const FACTOR: f64 = 0.40;
    (CONSTANT + (depth.min(32) as f64).ln() * (move_count.min(32) as f64).ln() * FACTOR) as usize
} else {
    0
};

As usual I also have a bunch of guard statements, like don’t reduce in check, don’t reduce captures, promotions in low depths, etc. The factor and constant is different between engines, and I had to run a bunch of tests to pick out the perfect value for my engine.

Engine     | Constant | Factor
---------- | -------- | ------
Ethereal   |     2.78 |   0.40
Weiss      |     1.65 |   0.35
Viridithas |     2.75 |   0.43
Stormphrax |     1.85 |   0.47
Titan*^    |     0.89 |   0.50
Obsidian   |     1.48 |   0.52
ice4*^     |     0.33 |   0.65

*does not have pv condition
^does not have improving condition
note: normalized to `r -= pv`, `r -= improving` forms

After running SPRTs on versions of my engine with all these constants and factors, I ended up picking the Ethereal LMR for my engine.

Search extensions

This is a pretty simple feature, if we are in a position where we are in check, increase depth by one to get out of the check, but limit the extensions to not completely nuke performance.

What is search instability?

I’ve mentioned search instability a few times, so I think it would be appropriate to elaborate a little bit. Search instability is when two searches from the same position can give contradicting results, from different bounds. For example if a null-window search fails low, yet a full window search wouldn’t have failed.

Search instability isn’t possible to avoid, if you have forward pruning techniques, but unless you have some severe bugs in your engine, or have tuned it very badly, it shouldn’t affect your performance too severely.

UCI

To let chess engines communicate with the outside world, I have implemented a subset of the Universal Chess Interface, so that I can connect it to SPRTs and online chess websites like lichess. To make a working UCI, you don’t need too many commands, and it’s pretty simple to implement. There are a few more instructions that are essentially no-ops like uci and isready, but here are the important ones:

position (fen [fenstring]| startpos) [moves (moves..)]

Sets position from the fenstring/startpos, and do each move afters (moves), moves are represented with from-to-square in algebraic notation, with an extra character added at the end for pawn promotions.

go [wtime [ms] btime [ms] winc [ms] binc [ms]]

Ask engine for best move. Addition time arguments can be given: wtime, btime, winc and binc, to show how much time and increment the engine has left to make it’s decision.

SPRTs

To test if my updates actually improve the engine, I can’t just play against it and judge through intuition. First of all i’m not very good at chess, second of all a lot of updates will only improve the engine subtly and will small elo differences. Also I need to tune the values such as the reduction constant on the null moves, to the optimal value.

The solution for this are SPRTs, Sequential Probability Ratio Tests, that will run the engine against a previous version of itself hundreds of times, and return an elo difference and a Likelyhood of Superiority (LOS). The higher the LOS, the more confident I can be in my changes to the engine. There are several SPRT providers, the most popular being fastchess, openbench and cutechess-cli.

Openbench is what many super professional engines use (or custom tests like fishtest for stockfish) but takes a lot more energy to set up, and fastchess is good enough for, so fastchess was good enough for my usecase. Openbench is a distributed testing setup and can be run on the cloud, and uses a web-based UI, while fastchess is a small cli application.

Intresting issues I encountered (debugging hell)

LMR Overflow

Usually rust will catch integer overflows, but I always compile with max optimizations and everything because I need my chess engine to always perform as fast as possible. So when I forgot to check for overflows, in some positions it would try to reduce further than even possible.

// Null window search
score = -self.negascout(
    board,
    mg,
    start_time,
    duration,
    -(alpha + 1),
    -alpha,
    depth - 1 - reduction, // If reduction is too big it will make depth usize_max..
    ply + 1,
);

This led to some very freaky flamegraphs

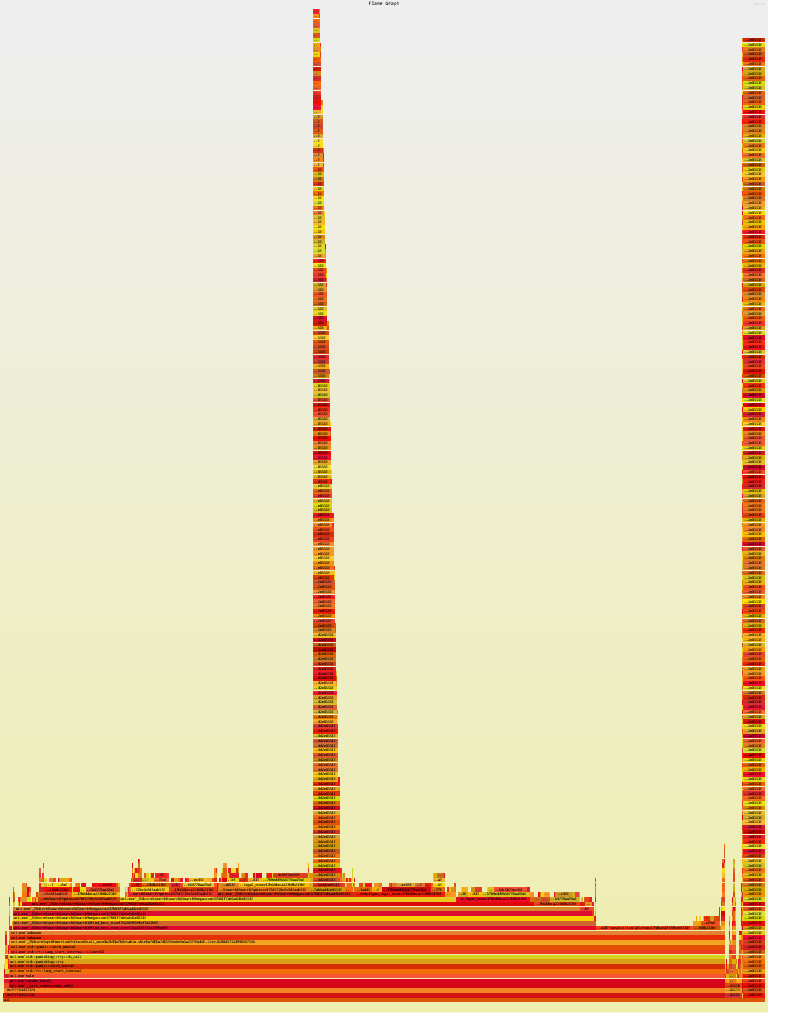
The fix was just a simple check for reduction, but trust me this took so much of my time and energy to find and fix, especially since this overflow was kind-of triggered non-deterministically.

// Make it not be larger than depth - 1 (otherwise it tries to subtract with overflow)
reduction = reduction.min(depth - 1);

Conclusion

Building the chess engine has been one of the most rewarding projects, and a massive rabbithole. I have learned a lot about low-level optimizations and the tradeoff between performance and stability.

While this engine is better than the vast majority of humans (2000+ elo), there is still room for improvement. Future plans include improving move generation with magic bitboards, and adding neural-network based evaluation to the engine for deeper insights, and to learn more about the programming of neural networks.

I hope this guide inspires others to take a look at chess programming, as it is a very challenging yet very instructive endeavor.

Resources

Algorithms Explained - minimax and alpha-beta pruning - Sebastian Lague
The Chess Programming Wiki, and amazing resource that covers everything about chess programming and more.
The Fascinating Programming of a Chess Engine - Bartek Spitza, an amazing video introductions to bitboards and alpha-beta pruning.
Description of the Universal Chess Interface - Shredder Chess

Building a Chess Engine in Rust